We start off by templating our kernel with parameters determined at run-time, and defining several constants.

‍

template <int InputChannels, int InputLength, int Padding, int KernelSize,  
int ChannelsPerThread>  
__global__ void conv1d(float *d_input, float *d_weight, float *d_bias, float *d_output)  
{  
   constexpr int SharedMemLength = constexpr_max(InputLength, KernelSize);  
   const int blockId = blockIdx.x;  
   const int tdIdx = threadIdx.x;  
   const int laneIdx = threadIdx.x % warpSize;  
   const int warpIdx = threadIdx.x / warpSize;  
   const int input_accesses_per_thread = (InputChannels * InputLength)/(4 * blockDim.x);  
   const int weight_accesses_per_thread = (InputChannels * KernelSize)/(blockDim.x);  
   const int weight_offset = blockId * InputChannels * KernelSize;  
   const int padded_input_length =  
   InputLength + Padding * 2;  
   const int shared_mem_offset_denom =  
   (InputLength * ChannelsPerThread) < 32 ? 32 : (InputLength * ChannelsPerThread);  
}

‍

Note that addition of a new template parameter, ‘ChannelsPerThread’. We search over different configurations of input tensor shape and channels per thread to find a value that minimizes run-time (more on this later). Next we define several constants for which I have included a natural language description below.

• blockID - Index for current block.
• tdIDx - Index for current thread within the block
• laneIdx - Index for thread within the warp
• warpIdx - Index for warp within the block (for example, first 32 threads in the block are warp 0)
• input_accesses_per_thread - The number of global memory load instructions that each thread has to issue to load the input from global memory to shared memory. This is a function of the size of the input (InputChannels * InputLength) divided by 4 times the number of threads in the block (blockDim.x). We multiply by four since we’ll be performing vectorized float4 loads.
• weight_accesses_per_thread - Same idea as previous but for the weights of the convolution filters. No dividing by four this time because loading of weights does not involve vectorized instructions.
• weight_offset/padded_input_length - Same as unoptimized kernel.
• shared_mem_offset_denom - This is the denominator that helps us calculate the shared memory load/store values after accounting for padding that helps eliminate bank conflicts.

With these defined, we move onto static memory allocations of registers and shared memory.

‍

//static mem allocations
float regInput[padded_input_length*ChannelsPerThread] = {0};
float regFilter[KernelSize*ChannelsPerThread];
__shared__ float shared_mem[InputChannels * SharedMemLength];

‍


Not much is different here from the unoptimized kernel, except that we modify the register allocations to account for the possibility of having multiple channels per thread. There's actually a minor bug related to memory allocation for shared memory in the code above.

‍

for (int channelIndex = 0; channelIndex < input_accesses_per_thread; ++channelIndex){
    int td_offset = 4 * (channelIndex * blockDim.x + tdIdx);
    int smem_offset = td_offset/shared_mem_offset_denom;
    float4 data = *reinterpret_cast<float4*>(&d_input[td_offset]);
    shared_mem[td_offset + smem_offset + 0] = data.x;
    shared_mem[td_offset + smem_offset + 1] = data.y;
    shared_mem[td_offset + smem_offset + 2] = data.z;
    shared_mem[td_offset + smem_offset + 3] = data.w;
}
__syncthreads();

‍

The new loading scheme for the input tensor from global memory to shared memory has several changes from what we did in the last post.

1. Instead of loading input values directly from global memory into thread registers, we use shared memory as an intermediary store. In doing so threads in the same warp can access sequential global memory addresses and the hardware can better utilize the cache-lines being loaded from global memory.
2. Instead of loading InputLength worth of elements per thread, we use our predefined ‘input_accesses_per_thread’ constant to allow for cases where each thread is responsible for multiple input channels worth of input elements.
3. We cast the pointer for d_input into one that is of type ‘float4’. This allows us to load 4 floats with a single instruction, and we confirm this by seeing that the LDG.E instruction in the compiled SASS is now a LDG.E.128. Note this doesn’t actually make the load from global memory faster, it just results in lower instruction overhead (decoding/fetch/etc) and helps alleviate warp stalls from choked instruction queues on the LD/ST units.
4. We offset the shared memory store index to prevent shared memory bank conflicts. Since each element in shared memory has to be stored in one of 32 banks, certain store patterns can result in multiple threads in the same warp accessing the same bank in the same cycle. Lets take a look at how the shared memory banks would look in a case where we do not pad shared memory.

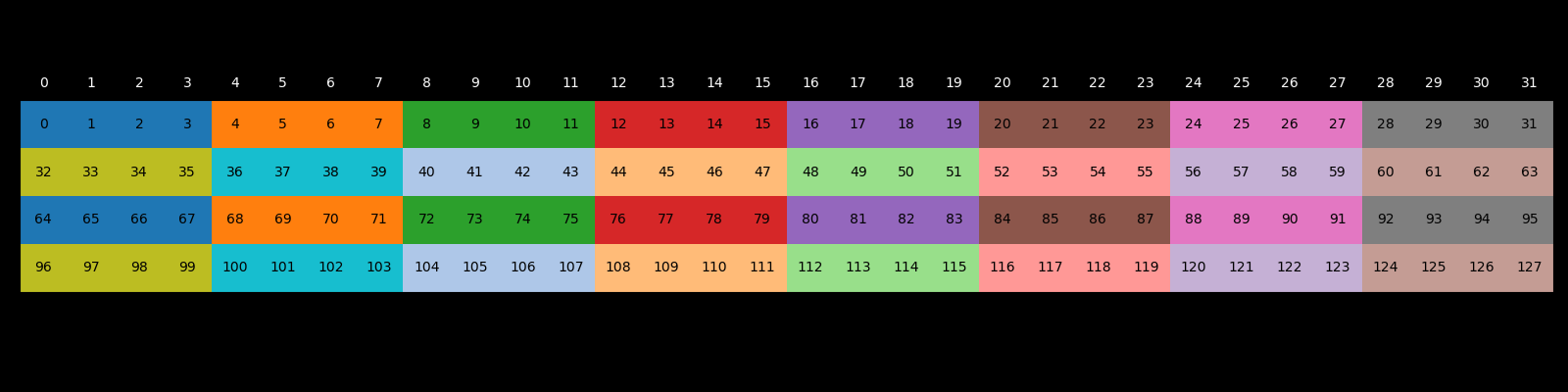
The image above shows what loading would like if each thread in a warp was responsible for loading 4 elements. Notice that at banks 0, 4, 8, 12, 16, 20, 24, and 28, multiple threads have the first element of their 4-element sequence. With no modifications, we would see shared memory bank conflicts during run-time as four separate threads in a warp would attempt to load from these banks. By adding a padding of size 1 every 32 elements, however, we can offset the bank for which the first element lies and eliminate this conflict. Now the first (and each sequential) element that threads in a warp try to access are all located in a separate bank.

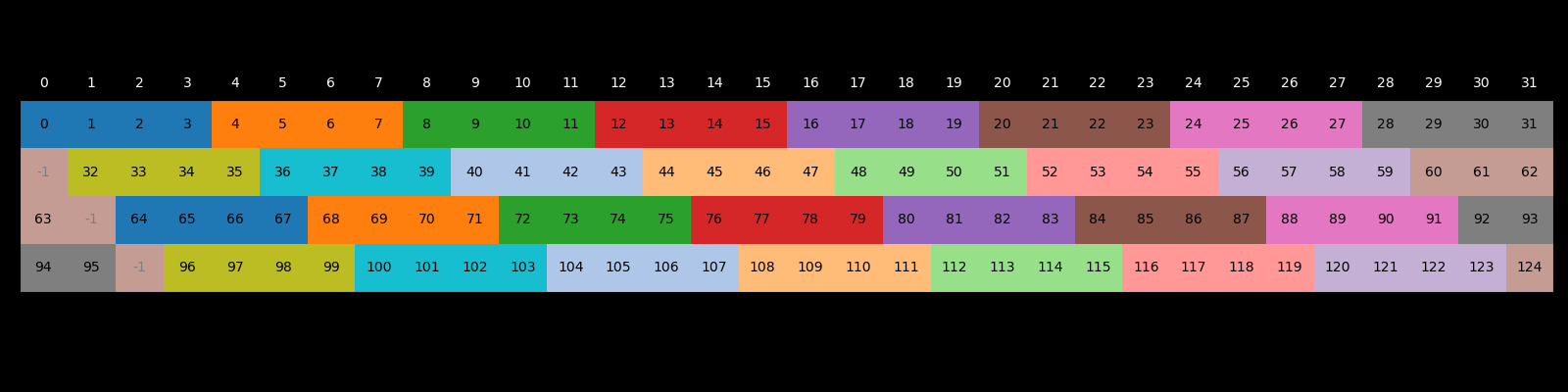
Next, we take the input elements from shared memory and load them into each threads registers. We don’t use vectorized loads here because those only work when the shared memory addresses are aligned with the data type, and shared memory padding ruins the alignment required for a float4 load. Also notice that we have added an outer loop to account for cases where each thread loads multiple channels.

‍

for (int channelIndex = 0; channelIndex < ChannelsPerThread; ++channelIndex){
    for (int colIndex = 0; colIndex < InputLength; ++colIndex){
        int regIndex = Padding + channelIndex * padded_input_length + colIndex;
        int sharedMemIndex = InputLength * (ChannelsPerThread * tdIdx + channelIndex) + colIndex;
        int smem_offset = sharedMemIndex/shared_mem_offset_denom;
        regInput[regIndex] = shared_mem[sharedMemIndex + smem_offset];
    }
}
__syncthreads();

‍


Our loading sequence for the convolution kernel weights only differentiates from the unoptimized version in that it uses shared memory as an intermediary store to coalesce global memory load. Using vectorized loads for the global memory → shared memory segment is tricky because the kernel length for all layer is 5, which doesn’t dice cleanly with a float4 or float2 load. Technically, since the size of the full kernel tensor (input_channels * kernel_size, 5120 for all layers in my case) is divisible 4, we could use a float4 load if the block size wasn’t 1024 or 512, but I chose to not bother because a few blocks are that size and I didn’t want to drive complexity.

‍‍

for (int channelIndex = 0; channelIndex < weight_accesses_per_thread; ++channelIndex){
    int td_offset = (channelIndex * blockDim.x) + tdIdx;
    shared_mem[td_offset] = d_weight[td_offset + weight_offset];
}
__syncthreads();

‍

The loading sequence from shared memory to thread registers for the convolution kernel is also pretty straight forward.

‍

for (int channelIndex = 0; channelIndex < ChannelsPerThread; ++channelIndex){
    for (int colIdx = 0; colIdx < KernelSize; ++colIdx){
        int regIndex = channelIndex * KernelSize + colIdx;
        int sharedMemIndex = KernelSize * (ChannelsPerThread * tdIdx + channelIndex) + colIdx;
        regFilter[regIndex] = shared_mem[sharedMemIndex];
    }
}

‍


I didn’t try to eliminate shared memory bank conflicts here because of two reasons. One, each thread loads a sequential chunk that is a multiple of 5, while in the input tensor load these chunks were a multiple of 4. Four is worse for bank conflicts because it dices 32 cleanly, whereas 5 results in fewer conflicts. Technically we still should have some, but they actually don’t show up in the NCU profiler. Secondly, as well will soon see, we are pretty close to the roofline already and optimizing further has sharp diminishing returns.

‍

//outer loop iterates over each element in output vector
for (int tileIdx = 0; tileIdx < InputLength; ++tileIdx){
    float res = 0.0;
    //inner loop performs dot product over all kernel positions and accumulates results
    for(int dotIdx = 0; dotIdx < KernelSize; ++dotIdx){
        for(int channelIndex = 0; channelIndex < ChannelsPerThread; ++channelIndex){
            res += regInput[tileIdx + dotIdx + (channelIndex * padded_input_length)] * regFilter[dotIdx + (channelIndex * KernelSize)];
        }
    }
    for (int offset = warpSize / 2; offset > 0; offset /= 2) {
        res += __shfl_down_sync(0xffffffff, res, offset);
    if (threadIdx.x == 0) {
        atomicAdd(&d_output[blockIdx.x * InputLength + tileIdx], d_bias[blockIdx.x]);
    }
    if (laneIdx == 0) {
        atomicAdd(&d_output[blockIdx.x * InputLength + tileIdx], res);
    }
}

‍


The main loop where arithmetic happens has changed a fair bit from our previous kernel.

1. The inner loop that performs the dot product has an additional inner-loop to support accumulation over multiple channels per thread. This also unlocks greater instruction level precision as all the fused multiply accumulates are independent of each other.
2. The sum-reduction required to calculate the final output value has changed quite a bit. Previously each warp wrote its accumulated result to shared memory, and a single for-loop (that all threads in the block ran) allowed for the block-level reduction.

for (int s = blockDim.x / 2; s > 0; s >>= 1) {
    if (threadIdx.x < s) {
        sumReduce[threadIdx.x] += sumReduce[threadIdx.x + s];
    }
    __syncthreads();
}

‍


The issue here is the if-statement which causes most threads to remain inactive during the reduction. In the first iteration only half of the block participates, only a quarter in the next iteration, etc. Near the end a huge number of warps are hitting barrier stalls. Our new approach involves using warp-level instrinsics to perform a warp-wide sum reduction, and global memory atomic adds to asynchronously sum values between different warps in a block.

‍

for (int offset = warpSize / 2; offset > 0; offset /= 2) {
    res += __shfl_down_sync(0xffffffff, res, offset);
}
if (threadIdx.x == 0) {
    atomicAdd(&d_output[blockIdx.x * InputLength + tileIdx], d_bias[blockIdx.x]);
}
if (laneIdx == 0) {
    atomicAdd(&d_output[blockIdx.x * InputLength + tileIdx], res);
}

‍


The for-loop now performs a warp-level reduction use the __shulf_down_sync() function call. After the warp shuffle is complete, the first thread in each warp adds its reduced value to global memory with an atomic add. Atomic adds are global memory writes that enable a thread to add to a global memory address with a lock that prevents race conditions. These are relatively slow operations but relatively few occur since we can’t have more than 32 warps in a block. The huge win these unlock is the elimination of any ‘syncthreads()’ calls, eliminating barrier stalls. Additionally, the use of warp-shuffles is much faster than repeated shared memory accesses (as done previously).

The final optimization for our new kernel is to run a sweep over the ‘channels-per-thread’ parameter to determine the optimal value for each unique tensor shape. Benefits of a larger number of channels per thread include greater ILP, smaller block sizes which can improve occupancy, as well as lower thread launch overhead. With a larger number of channels-per-thread also comes more register pressure and potentially register spilling to global memory.

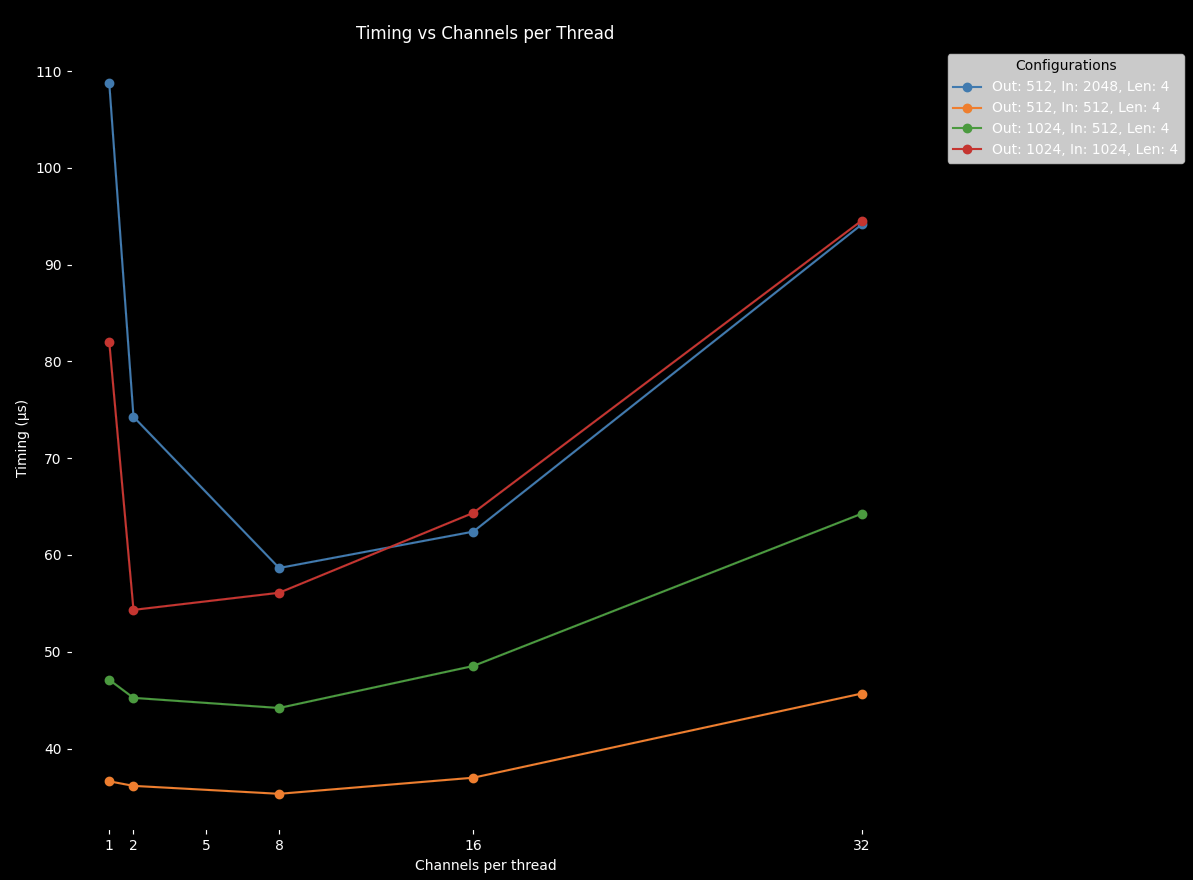
In general, inputs with a larger number of channels tend to benefit more when assigned a higher channel per thread count. The full mapping of input configurations for our U-Net and the tuned channels-per-thread value is below. We will make use of this in a later post when integrating our custom kernels with Pytorch.

Lets zoom out a bit to evaluate how well our program is doing based on a theoretical and empirical roof-line analysis. Recall arithmetic intensity is a function of how many FLOPs we perform for every byte we load. For a simplified 1D convolution with only one input channel, one output channel, and input length equal to output length, we perform K multiplies and K-1 adds for every output element.

The simplified FLOPs calculation can be expressed as follows:

$$
FLOPs_{\text{simplified}} = (K + K - 1) \cdot L = (2K - 1) \cdot L
$$

where \( K \) is the kernel size and \( L \) is the length of the input.

For multiple input/output channels, incorporating reductions for every output element and scaling by the number of output channels, the FLOPs calculation becomes:

$$
FLOPs = (2K - 1) \cdot L \cdot I + L \cdot (I - 1) = L \cdot ((2K - 1) \cdot I + (I - 1)) \cdot O
$$

where \( I \) is the number of input channels and \( O \) is the number of output channels.

Considering the memory load for both the input tensor and the kernel weights, where the input tensor is loaded once and kernel weights are loaded per output channel, the Bytes calculation is:

$$
Bytes = 4 \text{ Bytes/Element} \cdot I \cdot (K \cdot O + L)
$$

This leads to the final arithmetic intensity formula:

$$
\frac{FLOPs}{Bytes} = \frac{L \cdot ((2K - 1) \cdot I + (I - 1))}{I \cdot (K + L)}
$$

The most common configuration in our U-Net has a length of 4, 1024 input_channels, and 1024 output channels. Plugging these into our AI equations gives us an intensity of ~2. Referencing our roofline plot for the RTX 3090, we see that the theroetical light speed of our program is ~2 TFLOPs/s. Using our equation for FLOPs above, and the theoretical maximum FLOPs/s we find that the theoertical lower bound on kernel run time for a configuration of (1024, 1024, 4) is ~20microseconds.

Using the NCU profiler we find our kernel has a run-time of 34 uS. We can look at an empirical roofline analyses for our kernel.

The memory workload analysis also shows we achieved a memory throughput of 614 GB/s. The device chart below shows the breakdown of memory movement in the GPU.

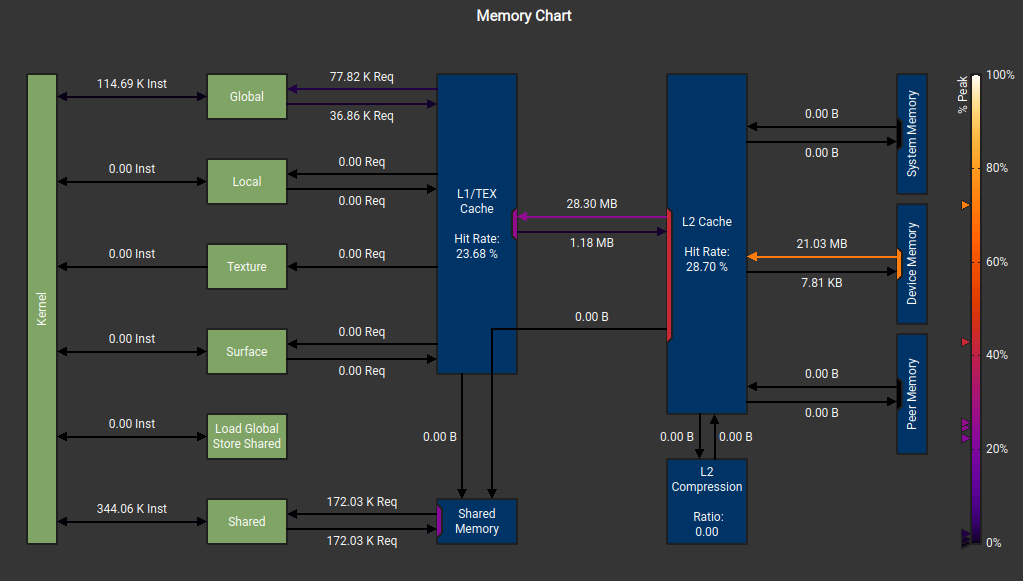
From all of the above, we can derive the table below.

‍

Its really cool to see how well our theoretical analysis maps to actual numbers from the profiler in terms of FLOPs/AI/etc. I did my best to explain the discrepancies and main takeaways in the points below.

• We load roughly the same number of bytes from global memory as we would expect in theory, but end up conducting ~3M more FLOPs than we expect. I believe these auxiliary ops come from things like indexing, type-casting, conditional branching, etc. I would expect this overhead to matter less in larger kernels but since this is a small kernel it is ~6% of total FLOPs.
• Our actual AI ends up being slightly higher than theoretical also due to these auxiliary FLOPs.
• We achieve ~65% of the theoretical device memory throughput for an RTX 3090. A Citadel micro-architecture analysis of Volta showed them only being able to reach about 80% of theoeretical so what we have is not terrible. Our runtime and FLOPs/s (also ~65% of theoretical) seem to be driven entirely by the memory bound nature of our kernel. I took away the shared memory bank-conflict avoidance logic and went back to the naive reduction from the first kernel and found a neglible change in runtime! Realizing how important memory bandwidth was to the kernel's performance, I went back to take a closer look at the earlier channel sweep since I was under the impression that the ChannelsPerThread number should only affect compute characteristics, not memory loading. I found, howeveer, that the slower kernels indeed had much lower global mem bandwidth on NCU. I am chalking this up to the 'sync_threads' in between loading of the weights and input tensors. More threads -> more sync overhead. A potential future improvement could be to use separate shared memory stores for the weights and input, so that loading of both can occur concurrently. Also, in hindsight, I should have ate the complexity associated with vectorized load instructions for the weights and implemented that optimization to get better GMEM bandwidth.

‍

‍