Kernel fusion refers to combining instructions for two (or more) distinct operations into a single GPU kernel [1]. As we learned when optimizing the 1D convolution kernel, for low arithmetic intensity workloads global memory bandwidth is the fundamental performance limiter. For that reason, you really really want to avoid writing stuff to device memory and having to read it back. A simple example would be a kernel that does \(A + B = C\), by loading \(A\) and \(B\) from GMEM, and writing \(C\) back. Then does \(C + D = E\), by loading \(C\) and \(D\) from GMEM, and writing \(E\) back. This sequence results in 4 loads, and 2 stores. If instead we fused this into a single operation such that \(A + B + D = E\), we would only have 3 loads and 1 store, saving ourselves from having to perform many unnecessary global memory reads and writes. For very small inference workloads (like ours), kernel launch overhead can also be non-trivial and reduced via kernel fusion.

There are limitations to how many operations can be fused. When a sequence of operations has intermediate results that are larger than can be stored on the shared memory of a single streaming multi-processor, they can generally not be fused. In this case, the only way for the intermediate value to be processed is with the write-back of the output to global memory and the triggering of the next kernel with the intermediate value as an input.

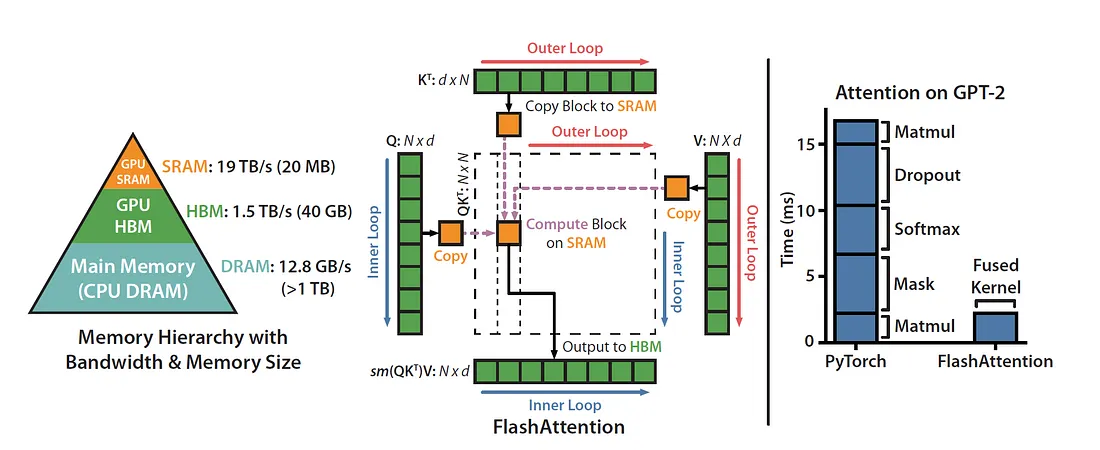
A pretty famous Attention optimization (Flash Attention) involved fusing all Attention operations into a single kernel and resulted in massive gains in inference latency for transformers [2]. You might wonder why this was implemented in 2022 and not 2017. I believe in large part, it’s because naive Softmax requires a reduction over the entire \(Q \cdot K^T\) matrix and performing this reduction in a single block does not solve for memory capacity of a single streaming multi-processor. Tri Dao realized in 2022 that you can use the Online Softmax trick to get around this bottleneck and perform all attention related computations in a single block using only a single read from global memory. While the online softmax trick came out in 2018, putting all the pieces together and implementing it in CUDA is non-trivial and requires a pretty deep algorithms & systems understanding of the Attention mechanism.

‍

Group Norm & Mish Fusion

The Conv1D block which makes up the majority of our U-Net consists of a 1D convolution, followed by Group Normalization and a Mish activation function. This sequence of operations (norm + activation) is the most common target for kernel fusion in deep learning workloads. In our case this fusion isn’t nearly as impactful as Flash Attention (or similar) because the size of the tensors being loaded for normalization & activation is pretty small. It’s also worth noting that Pytorch compile can also handle this fusing, but I decided to write my own kernel for learning purposes. Before going over the kernel, lets review the math associated with group norm and mish.

Group Normalization [3]

Group Norm was published in He et al. in 2018 as an alternative to batch normalization. A big issue with BN is sensitivity to batch size (see below). When normalizing over the batch dimension, batch statistics can become inaccurate and lead to increased model error.

‍

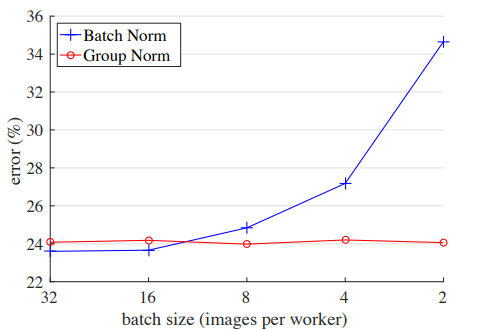
Additionally, at inference time the scale and shift value computed from the training dataset may no appropriately represent the input distribution and lead to poorer predictions. Group Norm addresses these issues by dividing channels into groups and calculating normalization statistics within each group.

‍

‍

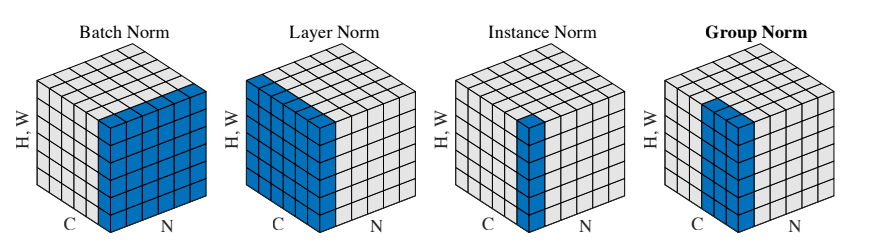
For our U-Net, the group size is 8 across all layers so we calculate in chunks of input_channel_dim/8. The normalization within the group is formulated similarly to other normalization schemes: we calculate the mean & variance for the set, then use these to scale values in the set accordingly.

\[
\mu_i = \frac{1}{m} \sum_{k \in S_i} x_k,
\]

\[
\sigma_i = \sqrt{ \frac{1}{m} \sum_{k \in S_i} (x_k - \mu_i)^2 + \epsilon },
\]

\[
\hat{x}_i = \frac{1}{\sigma_i} (x_i - \mu_i).
\]

Finally, the normalized value is scaled according to a learned parameter gamma and summed with another learned value beta. Each channel has its own unique gamma and beta. The idea behind these is to give gradient descent the ability to optimize the normalization scheme if it's beneficial.

\[
y_i = \gamma \hat{x}_i + \beta,
\]

‍

Mish Activation [4]

Mish is an a non-monotonic activation function developed by Diganta Misra to improve the training dynamics of large neural networks [?].

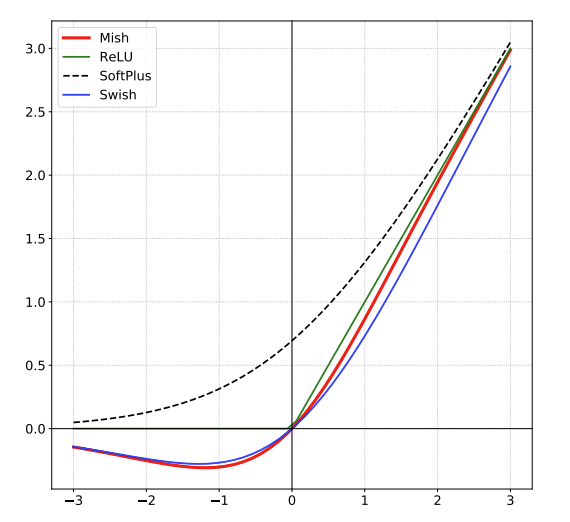
The idea here is to have a more continuous function to prevent dying ReLu's, a phenomena where a neuron's activation function causes a 0 output for all inputs, resulting in 0 gradient flow through the neuron and possibly stunted learning. The authors also claim that Mish results in a smoother loss landscape.

Mish is applied as the product of tanh and softplus(x).

\[
\text{Mish}(x) = x \cdot \tanh(\log(1 + e^x))
\]

Fused GroupNorm + Mish Kernel

The fused kernel for group normalization + mish activation is pretty straightforward, so I’ll let the comments in the code below do most of the explaining. In all input configurations, we launch kernels with 8 blocks so that normalization information can remain local to the block. The number of threads per block is a function of (input_channels * input_length)/8, since we have 8 groups and each block is responsible for 1/8th of the input. The actual kernel involves calculating the mean (using a reduction in shared memory), sum of squares (also a shared memory reduction), and saving the final normalized value back to global memory after adjusting for weight/bias/activation.

template <int CHUNK_SIZE>
__global__ void parallelGroupNormMishKernel(float* d_input, float* d_output, float* d_weights, float* d_bias, const int input_length) {
    const int tid = threadIdx.x;
    const int bid = blockIdx.x;
    __shared__ float sharedSum[CHUNK_SIZE]; // Shared memory for storing sum and sum of squares

    //1. Load data into shared memory
    float dataValue = d_input[bid * CHUNK_SIZE + tid]; 
    sharedSum[tid] = dataValue;
    __syncthreads();

    //2. Reduction to compute total sum (mean calculation)
    for (int stride = blockDim.x / 2; stride > 0; stride >>= 1) {
        if (tid < stride) {
            sharedSum[tid] += sharedSum[tid + stride];
        }
        __syncthreads();
    }

    //3. calculates the square of the difference between the value for the current thread and the mean for the group
    float mean = sharedSum[0] / CHUNK_SIZE;
    float diff = dataValue - mean;
    sharedSum[tid] = diff * diff; //save the squared difference in shared memory
    __syncthreads();

    //4. Reduction to compute total sum of squares (variance calculation)
    for (int stride = blockDim.x / 2; stride > 0; stride >>= 1) {
        if (tid < stride) {
            sharedSum[tid] += sharedSum[tid + stride];
        }
        __syncthreads();
    }

    //5. calculates the normalized value
    float variance = sharedSum[0] / CHUNK_SIZE;
    int global_td = bid * CHUNK_SIZE + tid;
    int weight_bias_idx = global_td / input_length;
    float invStdDev = rsqrtf(variance + 1e-5); // Using epsilon = 1e-5
     float normVal = (dataValue - mean) * invStdDev;
    
    //6. scale normalized value by weight and bias
    float weightedNormVal = normVal * d_weights[weight_bias_idx] + d_bias[weight_bias_idx];

    //7. apply Mish activation using CUDA special functions and store the result in global memory
    float mishVal = weightedNormVal * tanhf(log1pf(expf(weightedNormVal)));
    d_output[bid * CHUNK_SIZE + tid] = mishVal;
}

‍

References

[1] https://stackoverflow.com/questions/53305830/cuda-how-does-kernel-fusion-improve-performance-on-memory-bound-applications-on

[2] https://arxiv.org/pdf/2205.14135.pdf

[3] https://arxiv.org/abs/1803.08494

[4] https://arxiv.org/pdf/1908.08681.pdf